Định nghĩa, công thức, dạng bài tập phổ biến

Hình hộp chữ nhật được ứng dụng rất nhiều trong cuộc sống. Vì thế mà các dạng toán liên quan đến hình hộp chữ nhật cũng vì thế rất được coi trọng. Đây cũng là nhóm kiến thức nền tảng quan trọng để Học sinh có thể Học tốt các kiến thức về hình học không gian nâng cao. Hãy cùng Truonghoc247 tìm hiểu các kiến thức của hình hộp chữ nhật ngay sau đây nhé!

Hình hộp chữ nhật là gì?

Hình hộp chữ nhật là gì? Hãy cùng tìm hiểu ngay sau đây:

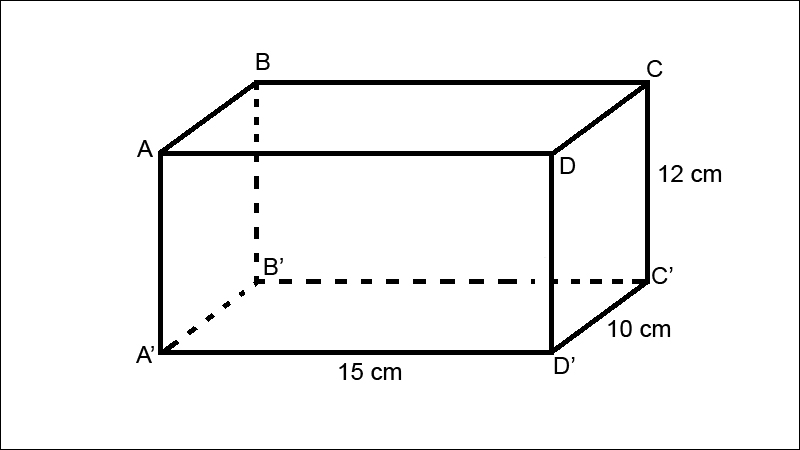
Định nghĩa hình hộp chữ nhật

Hình hộp chữ nhật là một hình không gian có 6 mặt đều là hình chữ nhật. Hai mặt đối diện nhau của hình chữ nhật được xem là hai mặt đáy của hình chữ nhật. Các mặt còn lại đều là mặt bên của hình chữ nhật.

Hình hộp chữ nhật tiếng anh là rectangular, phiên âm tiếng anh đọc là /rekˈtæŋ.ɡjə.lər/.

Tính chất hình hộp chữ nhật

Để nhận biết hình chữ nhật bạn có thể dựa theo các tính chất sau:

Hình chữ nhật sẽ có 12 cạnh, 8 đỉnh và 6 mặt.
Chu vi của hai mặt đối diện trong hình hộp chữ nhật bằng nhau.
Các đường chéo có hai đầu mút là 2 đỉnh đối nhau của hình hộp chữ nhật đồng quy tại một điểm.
Diện tích của hai mặt đối diện trong hình hộp chữ nhật là bằng nhau.

Xem thêm: Cách tính đường kính hình tròn và bài tập tự luyện tại nhà

Công thức liên quan đến hình hộp chữ nhật

Chu vi hình hộp chữ nhật

Chu vi hình hộp chữ nhật bằng tổng độ dài tất cả các cạnh bên và cạnh đáy của hình hộp chữ nhật: P = (a + b + h) * 4

Trong đó:

a là chiều dài hình hộp chữ nhật
b là chiều rộng hình hộp chữ nhật
h là chiều cao hình hộp chữ nhật

Diện tích xung quanh của hình hộp chữ nhật

Diện tích xung quanh hình hộp chữ nhật bằng tích của chu vi mặt đáy và chiều cao

Công thức tính: Sxq= 2 * h * (a + b)

Diện tích toàn phần của hình hộp chữ nhật

Diện tích toàn phần của hình hộp chữ nhật bằng tổng diện tích 6 mặt của hình hộp

Công thức tính diện tích toàn phần hình hộp chữ nhật: bằng tổng diện tích xung quanh của hình hộp chữ nhật và 2 mặt còn lại:

Stp= Sxq + S2 đáy

=> Stp= 2 * h * (a + b) +2 * a * b

Trong đó:

S gọi là diện tích hình hộp chữ nhật (diện tích xung quanh và diện tích toàn phần).
a gọi là chiều dài hình hộp chữ nhật.
b gọi là chiều rộng hình hộp chữ nhật.
h gọi là chiều cao hình hộp chữ nhật.

Công thức tính đường chéo hình hộp chữ nhật

Hình hộp chữ nhật có độ dài các đường chéo bằng nhau: d = √(a² + b² + c²)

Trong đó:

V gọi là thể tích hình hộp chữ nhật.
a gọi là chiều dài hình hộp chữ nhật.
b gọi là chiều rộng hình hộp chữ nhật.
h gọi là chiều cao hình hộp chữ nhật.

Công thức tính thể tích hình hộp chữ nhật

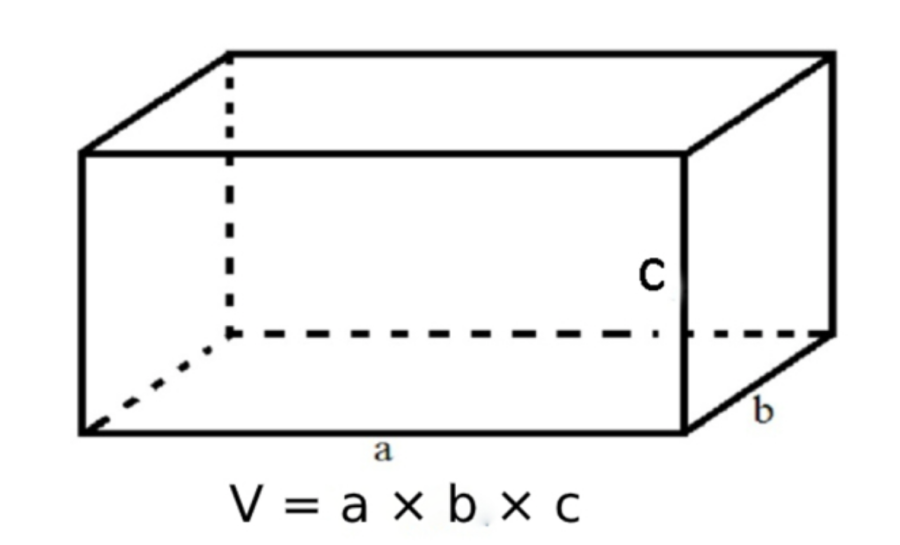
Thể tích hình hộp chữ nhật chính bằng lượng không gian mà hình chiếm, được tính bằng tích của diện tích đáy và chiều cao:

V = a * b * h

Trong đó:

V gọi là thể tích hình hộp chữ nhật.
a gọi là chiều dài hình hộp chữ nhật.
b gọi là chiều rộng hình hộp chữ nhật.
h gọi là chiều cao hình hộp chữ nhật.

Các dạng bài tập liên quan đến hình hộp chữ nhật

Truonghoc247 đã tổng hợp lại một số dạng bài tập phổ biến liên quan đến hình hộp chữ nhật đưới đây:

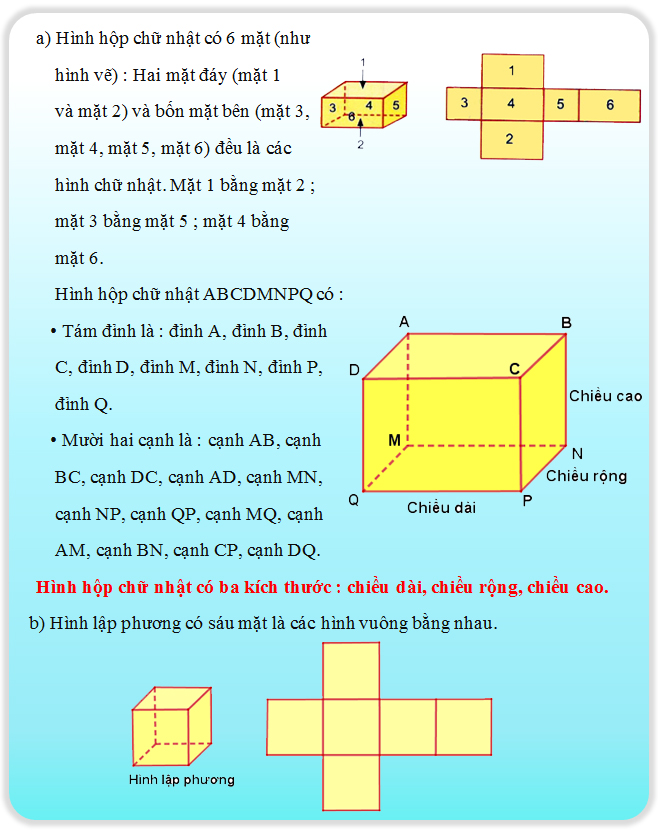
Dạng 1: Tính diện tích xung quanh hoặc diện tích toàn phần của hình hộp chữ nhật

Phương pháp: Áp dụng quy tắc tính diện tích xung quanh hoặc diện tích toàn phần.

Ví dụ: Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật có chiều dài 8cm, chiều rộng 6cm và chiều cao 4cm.

Bài giải:

Chu vi đáy của hình hộp chữ nhật là:

(8 + 6) × 2 = 28 (cm)

Diện tích xung quanh của hình hộp chữ nhật đó là:

28 × 4 = 112 (cm2)

Diện tích một đáy là:

8 × 6 = 48 (cm2)

Diện tích toàn phần của hình hộp chữ nhật đó là:

112 + 48 × 2 = 208(cm2)

Đáp số: Diện tích xung quanh: 112cm2

Diện tích toàn phần: 208cm2

Xem thêm: Công thức tính diện tích hình chữ nhật và các dạng bài thường gặp

Dạng 2: Biết diện tích xung quanh hoặc diện tích toàn phần, tìm chu vi đáy hoặc chiều cao của hình hộp chữ nhật

Phương pháp:

Từ công thức Sxq = (a + b) x 2 x h:

– Tìm chiều cao theo công thức: h = Sxq : [(a + b) x 2] = Sxq: (a + b) : 2;

– Tìm tổng chu vi đáy theo công thức: (a + b) x 2 = Sxq : h.

Nếu biết diện tích toàn phần ta cũng thay vào công thức để tìm các đại lượng chưa biết.

Ví dụ. Cho hình hộp chữ nhật có diện tích xung quanh là 217,5m2 và nửa chu vi mặt đáy bằng 14,5m. Tính chiều cao của hình hộp chữ nhật đó.

Bài giải:

Chu vi mặt đáy của hình hộp chữ nhật đó là:

14,5 × 2 = 29 (m)

Chiều cao của hình hộp chữ nhật đó là:

217,5 : 29 = 7,5 (m)

Đáp số: 7,5m

Dạng 3: Toán có lời văn (thường là tìm diện tích hộp, căn phòng, sơn tường …)

Phương pháp: Cần xác định xem diện tích cần tìm là diện tích xung quanh hay diện tích toàn phần rồi áp dụng quy tắc tính diện tích xung quanh hoặc diện tích toàn phần.

Ví dụ. Một căn phòng dạng hình hộp chữ nhật có chiều dài 6m, chiều rộng 48dm, chiều cao 4m. Người ta muốn quét vôi các bức tường xung quanh và trần của căn phòng đó. Hỏi diện tích cần quét vôi là bao nhiêu mét vuông, biết tổng diện tích các cửa bằng 12m2 (biết rằng chỉ quét vôi bên trong phòng)?

Bài giải:

Đổi 48dm = 4,8m

Diện tích xung quanh của căn phòng đó là:

(6 + 4,8) × 2 × 4 = 86,4 (m2)

Diện tích trần của căn phòng đó là:

6 × 4,8 = 28,8 (m2)

Diện tích cần quét vôi là:

86,4 + 28,8 – 12 = 103,2 (m2)

Đáp số: 103,2m2

Bài tập tự luyện về hình hộp chữ nhật

Bài 1. Cho hình hộp chữ nhật ABCD.A’B’C’D’

Những cạnh nào song song với DD’
Những cạnh nào song song với BC
Những cạnh nào song song với CD
Những mặt nào song song với BCC’B’

Bài giải

Các cạnh song song với DD’ là AA’, BB’, CC’
Các cạnh song song với BC là B’C’, AD, A’D’
Các cạnh song song với CD là AB, A’B’, C’D’
BCC’B’ // ADD’A’

Vì BCC’B’ chứa hai đường thảng BC và BB’ cắt nhau, mà BC // AD và BB’ // AA’

Bài 2. Một căn phòng dài 5m, rộng 3.2m và cao 3m. Người ta muốn quét vôi trần nhà và bốn bức tường. Biết rằng tổng diện tích các cửa là 6.3m2. Hãy tính diện tích cần quét vôi?

Bài giải

– Diện tích trần nhà là:

S1 = 5 . 3,2 = 16 m2

– Diện tích một mặt các bức tường của căn phòng là:

S2 = (3 . 5) + (3 . 3,2) . 2 = 49,2 m2

– Diện tích cần quét vôi căn phòng (đã trừ diện tích các cửa) là:

S = S1 + S2 – 6,3 = 16 + 49,2 – 6,3 = 68,8 m2

Bài 3. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 3cm, AD = 4cm, AA’ = 5cm. Tính AC’?

Bài giải

Ta có: AB = A’B’ = 3cm, AD = B’C’ = 4cm, AA’ = BB’ = 5cm

Áp dụng định lý pytago vào tam giác vuông A’B’C’, ta có:

A’C’ = căn bậc hai của (A’B’2 + B’C’2) = 5cm

Áp dụng định lý pitago vào tam giác vuông AA’C, ta có:

AC’ = 5 căn 2 cm

Vậy AC’ = 5 căn 2 cm

Bài 4. Cho hình hộp chữ nhật có chiều dài bằng 6cm, chiều rộng bằng 1/2 chiều dài và chiều cao gấp 3 lần chiều rộng. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình hộp chữ nhật đó.

Bài giải

Để tính được diện tích xung quanh, diện tích toàn phần, thể tích hình hộp chữ nhật, ta cần biết đầy đủ ba kích thước của nó là chiều dài, chiều rộng, chiều cao. Từ giả thiết, ta có:

a =6cm, b =1/2 a = 3cm, c = 3b = 9m

Khi đó:

– Diện tích xung quanh của hình hộp chữ nhật là:

Sxq = 2(a+b)c = 162cm2

– Diện tích toàn phần của hình hộp chữ nhật là:

Stp = Sxq + 2Sđ = 162 + 2 . 6 . 3 = 198 cm2

– Thể tích hình hộp chữ nhật là:

V = abc = 162 cm3

Bài 5. Một bể nước hình chữ nhật có chiều dài 2,5m. Lúc đầu bể không có nước. Sau khi đổ vào bể 140 thùng nước, mỗi thùng chứa 20 lít thì mực nước của bể là 0,8m.

a, Tính chiều rộng của bể nước

Người ta đổ thêm vào bể 60 thùng nước nữa thì đầy bể. Hỏi bể cao nhiêu mét?

Bài giải

Thể tích nước đổ vào bể đợt 1:

V1 = 20 . 140 = 2800 (l) = 2,8 m3

Chiều rộng của bể nước:

2,8 : (2,5 . 0,8) = 1,4 m

Tỷ số của mực nước tăng thêm so với mực nước đổ vào đợt 1:

V1/V2 = 60 /120 = 1/2

Mực nước tăng thêm là: 0,8 . 0,4 = 0,32 m

Độ cao của bể là: 0,8 + 0,32 = 1,12 m

Bài 6. Một hình hộp chữ nhật có tổng ba kích thước bằng 61cm và đường chéo bằng 37 cm. Tính diện tích toàn phần của hình hộp chữ nhật đó.

Bài giải

Gọi ba kích thước của hình hộp chữ nhật là a, b, c. Ta có:

a+b+c = 61 (1)

và a2 + b2 + c2 = 372 (2)

Vậy diện tích toàn phần của hình hộp chữ nhật là 2352 cm2

Bài 7. Cho hình hộp chữ nhật ABCD.A1B1C1D1. Biết AB = 3cm, AA1 = 6cm, và SA1C1C = 30cm2. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình hộp chữ nhật đó.

Bài giải

Ta có: AA1 song song và bằng BB1; BB1 song song và bằng CC1 => AA1 song song và bằng= CC1 => AA1C1C là hình bình hành

Ta lại có:

AA1 vuông góc với A1B1C1D1 => AA1 vuông góc với A1C1 ⇔ góc AA1C1 = 90°

Khi đó, hình bình hành AA1C1C có một góc vuông nên nó là hình chữ nhật.

Gọi S là diện tích của hình chữ nhật AA1C1C, ta có:

S = AA1 . AC <=> 30 = 6 . AC => AC = 5 cm

Áp dụng định lý pytago vào tam giác ABC, ta được:

BC = căn bậc hai (25 – 9) = 4cm

Khi đó:

– Diện tích xung quang hình hộp chữ nhật là:

Sxq = 2 (AB + BC) . AA1 = 84 cm2

– Diện tích toàn phần hình hộp chữ nhật là:

Stp = Sxq + 2Sđ = 84 + 2 . 3 . 4 = 108 cm2

– Thể tích của hình hộp chữ nhật là:

V = AB . BC . AA1 = 72 cm3

Bài 8. Một bình đựng nước có dạng hình hộp chữ nhật có chiều rộng bằng 4cm, chiều dài bằng 8cm, chiều cao bằng 5cm. Mực nước hiện tại bằng 8cm, chiều cao băng 5cm, Mực nước hiện tai bằng 3/4 chiều cao của bình. Nếu ta đổ nước trong bình khác hình lập phương có cạnh bằng 5 cm thì chiều cao mực nước là bao nhiêu?

Bài giải

Thể tích nước có trong hình hộp chữ nhật là:

V = 3/4 . 5 . 8 . 4 = 120 cm3

Gọi h là chiều cao của mực nước mới ở hình lập phương có cạnh là 5 cm, ta có:

h = V /25 = 120 /25 = 4,8 cm

Bài 9. Một hình hộp chữ nhật có thể tích bằng 60 cm3. Diện tích toàn phần bằng 91 cm2. Tính chiều rộng, chiều dài của hình hộp chữ nhật, biết chiều cao bằng 4cm

Bài giải

Gọi hai kích thước của hình hộp chữ nhật lần lượt là a và b

Ta có: V = 4 ab = 60 cm3

=> ab = 15 (1)

Lại có: Stp = Sxq + 2Sđ = 2ph + 2ab

Stp = 2(a+b).4 + 2ab = 94

Hay a + b = 8 (2)

Từ (1) v (2) => a = 5, b = 3 hoặc a=3, b = 5

Vậy hai kích thước của hình hộp chữ nhật là 3cm và 5cm

Bài 10. Tính các kích thước của hình hộp chữ nhật, biết rằng chúng tỷ lệ với 3, 4, 5 và thể tích của hình hộp này là 480 cm3

Bài giải

Gọi các kích thước của hình hộp là a, b, c

Theo giả thiết, ta có: a/3 = b/4 = c/5 và V = abc = 480 cm3

Theo tính chất dãy tỉ số bằng nhau, ta có:

k3 = abc/(3.4 . 5) = 480/60 = 8

=> k = 2

Vậy các kích thước của hình hộp chữ nhật là a = 6 cm, b = 8 cm, c = 10 cm

Ứng dụng tính thể tích hình hộp chữ nhật trong thực tế

Để tính thể tích hình hộp chữ nhật, cần xác định các đại lượng có trong công thức tính. Ví dụ, bạn muốn tính thể tích chứa nước của một bể bơi có dạng hình hộp chữ nhật, các bạn cần thực hiện các bước sau:

Bước 1: Xác định chiều dài của bể bơi

Chiều dài chính là cạnh dài nhất của mặt phẳng hình chữ nhật nằm ở phía trên dưới của hình hộp chữ nhật. Bạn có thể dùng thước dây để đo cạnh dài nhất của mặt bể bơi, ví dụ: chiều dài = 5 m.

Bước 2: Xác định chiều rộng của bể bơi

Chiều rộng là cạnh ngắn nhất của mặt phẳng hình chữ nhật nằm ở phía trên hay dưới của hình hộp chữ nhật. Bạn có thể dùng thước dây để đo cạnh ngắn nhất của mặt bể bơi, ví dụ: chiều rộng = 3 m.

Bước 3: Xác định chiều cao của bể bơi

Chiều cao là cạnh đứng vuông góc với chiều dài và chiều rộng của hình hộp chữ nhật. Bạn có thể đo chiều cao của bể bơi bằng thước dây, ví dụ: chiều cao = 1,5 m.

Bước 4: Tính tích số của ba đơn vị chiều dài, chiều rộng và chiều cao.

Bạn hãy nhân 3 đại lượng chiều rộng, chiều dài và chiều cao tùy ý, không cần quan tâm đến thứ tự trước, sau. Áp dụng công thức tính thể tích hình hộp chữ nhật cho bể bơi trên, ta có:

V = a * b * h = 5 * 3 * 1,5 = 22,5 (m3)

Kết luận: Bể bơi có thể chứa được thể tích nước là 22,5 (m3)

Hướng dẫn vẽ hình hộp chữ nhật nhanh chóng, chính xác

Bước 1: Vẽ mặt đáy dưới hình hộp chữ nhật: Vẽ 1 hình bình hành MNPQ bất kỳ trên giấy. Đây là đáy của hình hộp chữ nhật

Bước 2: Vẽ các đường cao: Từ 4 đỉnh hình bình hành lần lượt dóng 4 đường cao MA, NB, PC, QD sao cho MA và QD vuông góc với MQ, NB và PC vuông góc với NP

Lưu ý: NB, NM, NP vẽ nét đứt vì là phần đoạn thẳng bị lấp

Bước 3: Lần lượt nối các đỉnh A, B, C, D lại ta được hình hộp chữ nhật ABCD.MNPQ

Trên đây, Truonghoc247 đã cùng bạn tìm hiểu kiến thức của hình hộp chữ nhật. Hy vọng những thông tin chúng tôi cung cấp sẽ giúp bạn học tập hiệu quả hơn.

https%3A%2F%2Ftruonghoc247.vn%2Fhinh-hop-chu-nhat%2F